Решение систем линейных уравнений методом гаусса. Назначение метода Гаусса. Когда нет решений
Систему уравнений (1.1) представим в виде
Известно большое число схем метода исключения, приспособленных для ручного или машинного счета матриц общего или специального вида.
Метод Гаусса можно интерпретировать как метод, в котором первоначально матрица приводится к верхней треугольной форме (прямой ход), а далее - к единичной (обратный ход). Очевидно, что если матрица единичная, то x t = b r
Пусть матрица системы (1.3) - верхняя треугольная, поэтому a tj = 0 при i > j, т. е. все элементы ниже главной диагонали равны нулю. Тогда из последнего уравнения сразу определяем х п. Подставляя х п в предпоследнее уравнение, находим х а _ х и т. д. Общие формулы имеют вид
При k > I коэффициенты а ы = 0.
Приведем матрицу системы (1.3) к верхней треугольной. Вычтем из второго уравнения системы (1.3) первое, умноженное на такое число, при котором коэффициент при х х обратится в нуль. То же проделаем со всеми остальными уравнениями. В результате все коэффициенты первого столбца, лежащие ниже главной диагонали, обратятся в нуль. Затем, используя второе уравнение, обратим в нуль соответствующие коэффициенты второго столбца. Последовательно продолжая этот процесс, приведем матрицу системы к верхней треугольной форме.
Запишем общие формулы метода Гаусса. Пусть проведено исключение коэффициентов из (А - 1)-го столбца. Тогда останутся уравнения с ненулевыми элементами ниже главной диагонали:
Умножим k-ю строку на число с тк = т > k и вычтем
из m-й строки. Первый ненулевой элемент этой строки обратится в нуль, а остальные изменятся по формулам
Проведя вычисления по этим формулам при всех указанных индексах, обратим в нуль элементы k-ro столбца, лежащие ниже главной диагонали. Аналогичная процедура приводит матрицу системы к верхней треугольной форме, при этом весь процесс приведения называется ПРЯМЫМ ХОДОМ МЕТОДА ГАУССА. Вычисление неизвестных по формулам (1.4) называют ОБРАТНЫМ ХОДОМ метода.
Обратный ход можно совершить иначе, если обратить в нуль и все коэффициенты, лежащие выше главной диагонали. Например, элементы п -го столбца обращаются в нуль, если ej^| умножить на (-a^V ax t = б| 2л) , где Ь^ п) - коэффициенты правой части i-го уравнения после указанных преобразований.
На некотором шаге прямого хода может оказаться, что коэффициент aj*" * 0, но мал по сравнению с остальными элементами матрицы системы и, в частности, мал по сравнению с элементами первого столбца. Деление коэффициентов системы на малую величину может привести к значительным ошибкам округления.
Для уменьшения ошибок округления поступают следующим образом. Среди элементов первого столбца а ^ каждой промежуточной матрицы выбирают наибольший по модулю (главный) элемент и путем перестановки i-й строки со строкой, содержащей главный элемент, добиваются того, что главный элемент становится ведущим. Такая модификация метода исключения Гаусса называется методом Гаусса с выбором главного элемента. Случай появления нулевых элементов обходится при этом сам собой.
Для реализации метода требуется примерно п 3 /3 операций типа умножения и п 3 /3 операций типа сложения . Полезно помнить, что оценка числа операций определяется в основном операциями, затрачиваемыми при выполнении прямого хода метода Гаусса. Обратный ход метода Гаусса требует примерно п 2 операций. Следовательно, если требуется решить несколько систем линейных алгебраических уравнений вида Ах = b с одной и той же матрицей и различными правыми частями, то общее число операций при решении S систем будет оцениваться величиной (2/3)п 3 + Sn 2 . В этом случае целесообразно реализовать алгоритм метода Гаусса в виде двух подпрограмм: первая подпрограмма должна реализовывать прямой ход алгоритма и получать на выходе верхнюю треугольную матрицу, а вторая подпрограмма должна, используя полученную матрицу, вычислять решение системы для произвольной правой части.
Метод Гаусса, называемый также методом последовательного исключения неизвестных, состоит в следующем. При помощи элементарных преобразований систему линейных уравнений приводят к такому виду, чтобы её матрица из коэффициентов оказалась трапециевидной (то же самое, что треугольной или ступенчатой) или близкой к трапециевидной (прямой ход метода Гаусса, далее - просто прямой ход). Пример такой системы и её решения - на рисунке сверху.
В такой системе последнее уравнение содержит только одну переменную и её значение можно однозначно найти. Затем значение этой переменной подставляют в предыдущее уравнение (обратный ход метода Гаусса , далее - просто обратный ход), из которого находят предыдущую переменную, и так далее.
В трапециевидной (треугольной) системе, как видим, третье уравнение уже не содержит переменных y и x , а второе уравнение - переменной x .
После того, как матрица системы приняла трапециевидную форму, уже не представляет труда разобраться в вопросе о совместности системы, определить число решений и найти сами решения.
Преимущества метода:
- при решении систем линейных уравнений с числом уравнений и неизвестных более трёх метод Гаусса не такой громоздкий, как метод Крамера , поскольку при решении методом Гаусса необходимо меньше вычислений;
- методом Гаусса можно решать неопределённые системы линейных уравнений, то есть, имеющие общее решение (и мы разберём их на этом уроке), а, используя метод Крамера, можно лишь констатировать, что система неопределённа;
- можно решать системы линейных уравнений, в которых число неизвестных не равно числу уравнений (также разберём их на этом уроке);
- метод основан на элементарных (школьных) методах - методе подстановки неизвестных и методе сложения уравнений, которых мы коснулись в соответствующей статье.
Чтобы все прониклись простотой, с которой решаются трапециевидные (треугольные, ступенчатые) системы линейных уравнений, приведём решение такой системы с применением обратного хода. Быстрое решение этой системы было показано на картинке в начале урока.
Пример 1. Решить систему линейных уравнений, применяя обратный ход:
Решение. В данной трапециевидной системе переменная z однозначно находится из третьего уравнения. Подставляем её значение во второе уравнение и получаем значение переменой y :
Теперь нам известны значения уже двух переменных - z и y . Подставляем их в первое уравнение и получаем значение переменной x :
Из предыдущих шагов выписываем решение системы уравнений:
Чтобы получить такую трапециевидную систему линейных уравнений, которую мы решили очень просто, требуется применять прямой ход, связанный с элементарными преобразованиями системы линейных уравнений. Это также не очень сложно.
Элементарные преобразования системы линейных уравнений
Повторяя школьный метод алгебраического сложения уравнений системы, мы выяснили, что к одному из уравнений системы можно прибавлять другое уравнение системы, причём каждое из уравнений может быть умножено на некоторые числа. В результате получаем систему линейных уравнений, эквивалентную данной. В ней уже одно уравнение содержало только одну переменную, подставляя значение которой в другие уравнений, мы приходим к решению. Такое сложение - один из видов элементарного преобразования системы. При использовании метода Гаусса можем пользоваться несколькими видами преобразований.
На анимации выше показано, как система уравнений постепенно превращается в трапециевидную. То есть такую, которую вы видели на самой первой анимации и сами убедились в том, что из неё просто найти значения всех неизвестных. О том, как выполнить такое превращение и, конечно, примеры, пойдёт речь далее.
При решении систем линейных уравнений с любым числом уравнений и неизвестных в системе уравнений и в расширенной матрице системы можно :
- переставлять местами строки (это и было упомянуто в самом начале этой статьи);
- если в результате других преобразований появились равные или пропорциональные строки, их можно удалить, кроме одной;
- удалять "нулевые" строки, где все коэффициенты равны нулю;
- любую строку умножать или делить на некоторое число;
- к любой строке прибавлять другую строку, умноженное на некоторое число.
В результате преобразований получаем систему линейных уравнений, эквивалентную данной.
Алгоритм и примеры решения методом Гаусса системы линейных уравнений с квадратной матрицей системы
Рассмотрим сначала решение систем линейных уравений, в которых число неизвестных равно числу уравнений. Матрица такой системы - квадратная, то есть в ней число строк равно числу столбцов.
Пример 2. Решить методом Гаусса систему линейных уравнений
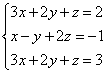
Решая системы линейных уравнений школьными способами, мы почленно умножали одно из уравнений на некоторое число, так, чтобы коэффициенты при первой переменной в двух уравнениях были противоположными числами. При сложении уравнений происходит исключение этой переменной. Аналогично действует и метод Гаусса.
Для упрощения внешнего вида решения составим расширенную матрицу системы :
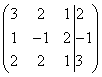
В этой матрице слева до вертикальной черты расположены коэффициенты при неизвестных, а справа после вертикальной черты - свободные члены.
Для удобства деления коэффициентов при переменных (чтобы получить деление на единицу) переставим местами первую и вторую строки матрицы системы . Получим систему, эквивалентную данной, так как в системе линейных уравнений можно переставлять местами уравнения:
С помощью нового первого уравнения исключим переменную x из второго и всех последующих уравнений . Для этого ко второй строке матрицы прибавим первую строку, умноженную на (в нашем случае на ), к третьей строке – первую строку, умноженную на (в нашем случае на ).
Это возможно, так как
Если бы в нашей системе уравнений было больше трёх, то следовало бы прибавлять и ко всем последующим уравнениям первую строку, умноженную на отношение соответствующих коэффициентов, взятых со знаком минус.
В результате получим матрицу эквивалентную данной системе новой системы уравнений, в которой все уравнения, начиная со второго не содержат переменнную x :
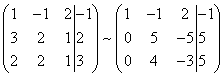
Для упрощения второй строки полученной системы умножим её на и получим вновь матрицу системы уравнений, эквивалентной данной системе:
Теперь, сохраняя первое уравнение полученной системы без изменений, с помощью второго уравнения исключаем переменную y из всех последующих уравнений. Для этого к третьей строке матрицы системы прибавим вторую строку, умноженную на (в нашем случае на ).
Если бы в нашей системе уравнений было больше трёх, то следовало бы прибавлять и ко всем последующим уравнениям вторую строку, умноженную на отношение соответствующих коэффициентов, взятых со знаком минус.
В результате вновь получим матрицу системы, эквивалентной данной системе линейных уравнений:
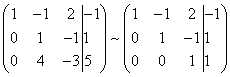
Мы получили эквивалентную данной трапециевидную систему линейных уравнений:
Если число уравнений и переменных больше, чем в нашем примере, то процесс последовательного исключения переменных продолжается до тех пор, пока матрица системы не станет трапециевидной, как в нашем демо-примере.
Решение найдём "с конца" - обратный ход
. Для этого из последнего уравнения определим z
:
.
Подставив это значение в предшествующее уравнение, найдём y
:
Из первого уравнения найдём x
:
Ответ: решение данной системы уравнений - 
.
: в этом случае будет выдан тот же ответ, если система имеет однозначное решение. Если же система имеет бесконечное множество решений, то таков будет и ответ, и это уже предмет пятой части этого урока.
Решить систему линейных уравнений методом Гаусса самостоятельно, а затем посмотреть решение
Перед нами вновь пример совместной и определённой системы линейных уравнений, в которой число уравнений равно числу неизвестных. Отличие от нашего демо-примера из алгоритма - здесь уже четыре уравнения и четыре неизвестных.
Пример 4. Решить систему линейных уравнений методом Гаусса:
Теперь нужно с помощью второго уравнения исключить переменную из последующих уравнений. Проведём подготовительные работы. Чтобы было удобнее с отношением коэффициентов, нужно получить единицу в во втором столбце второй строки. Для этого из второй строки вычтем третью, а полученную в результате вторую строку умножим на -1.
Проведём теперь собственно исключение переменной из третьего и четвёртого уравнений. Для этого к третьей строке прибавим вторую, умноженную на , а к четвёртой - вторую, умноженную на .
Теперь с помощью третьего уравнения исключим переменную из четвёртого уравнения. Для этого к четвёртой строке прибавим третью, умноженную на . Получаем расширенную матрицу трапециевидной формы.
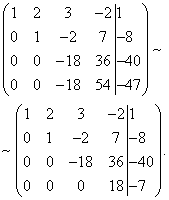
Получили систему уравнений, которой эквивалентна заданная система:
Следовательно, полученная и данная системы являются совместными и определёнными. Окончательное решение находим «с конца». Из четвёртого уравнения непосредственно можем выразить значение переменной "икс четвёртое":
Это значение подставляем в третье уравнение системы и получаем
,
,
Наконец, подстановка значений
В первое уравнение даёт
,
откуда находим "икс первое":
Ответ: данная система уравнений имеет единственное решение 
.
Проверить решение системы можно и на калькуляторе, решающем методом Крамера : в этом случае будет выдан тот же ответ, если система имеет однозначное решение.
Решение методом Гаусса прикладных задач на примере задачи на сплавы
Системы линейных уравнений применяются для моделирования реальных объектов физического мира. Решим одну из таких задач - на сплавы. Аналогичные задачи - задачи на смеси, стоимость или удельный вес отдельных товаров в группе товаров и тому подобные.
Пример 5. Три куска сплава имеют общую массу 150 кг. Первый сплав содержит 60% меди, второй - 30%, третий - 10%. При этом во втором и третьем сплавах вместе взятых меди на 28,4 кг меньше, чем в первом сплаве, а в третьем сплаве меди на 6,2 кг меньше, чем во втором. Найти массу каждого куска сплава.
Решение. Составляем систему линейных уравнений:
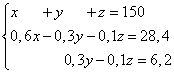
Умножаем второе и третье уравнения на 10, получаем эквивалентную систему линейных уравнений:
Составляем расширенную матрицу системы:
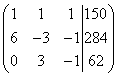
Внимание, прямой ход. Путём сложения (в нашем случае - вычитания) одной строки, умноженной на число (применяем два раза) с расширенной матрицей системы происходят следующие преобразования:
Прямой ход завершился. Получили расширенную матрицу трапециевидной формы.
Применяем обратный ход. Находим решение с конца. Видим, что .
Из второго уравнения находим
Из третьего уравнения -
Проверить решение системы можно и на калькуляторе, решающем методом Крамера : в этом случае будет выдан то же ответ, если система имеет однозначное решение.
О простоте метода Гаусса говорит хотя бы тот факт, что немецкому математику Карлу Фридриху Гауссу на его изобретение потребовалось лишь 15 минут. Кроме метода его имени из творчества Гаусса известно изречение "Не следует смешивать то, что нам кажется невероятным и неестественным, с абсолютно невозможным" - своего рода краткая инструкция по совершению открытий.
Во многих прикладных задачах может и не быть третьего ограничения, то есть, третьего уравнения, тогда приходится решать методом Гаусса систему двух уравнений с тремя неизвестными, или же, наоборот - неизвестных меньше, чем уравнений. К решению таких систем уравнений мы сейчас и приступим.
С помощью метода Гаусса можно установить, совместна или несовместна любая система n линейных уравнений с n переменными.
Метод Гаусса и системы линейных уравнений, имеющие бесконечное множество решений
Следующий пример - совместная, но неопределённая система линейных уравнений, то есть имеющая бесконечное множество решений.
После выполнения преобразований в расширенной матрице системы (перестановки строк, умножения и деления строк на некоторое число, прибавлению к одной строке другой) могли появиться строки вида
Если во всех уравнениях имеющих вид
Свободные члены равны нулю, то это означает, что система неопределённа, то есть имеет бесконечное множество решений, а уравнения этого вида – «лишние» и их исключаем из системы.
Пример 6.
Решение. Составим расширенную матрицу системы. Затем с помощью первого уравнения исключим переменную из последующих уравнений. Для этого ко второй, третьей и четвёртой строкам прибавим первую, умноженную соответственно на :
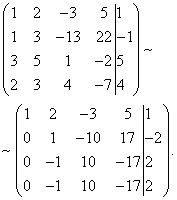
Теперь вторую строку прибавим к третьей и четвёртой.
В результате приходим к системе
Последние два уравнения превратились в уравнения вида . Эти уравнения удовлетворяются при любых значениях неизвестных и их можно отбросить.
Чтобы удовлетворить второму уравнению, мы можем для и
выбрать произвольные значения
, тогда значение для
определится уже однозначно: 
. Из первого уравнения
значение для также находится
однозначно: 
.
Как заданная, так и последняя системы совместны, но неопределённы, и формулы
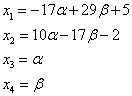
при произвольных и дают нам все решения заданной системы.
Метод Гаусса и системы линейных уравнений, не имеющие решений
Следующий пример - несовместная система линейных уравнений, то есть не имеющая решений. Ответ на такие задачи так и формулируется: система не имеет решений.
Как уже говорилось в связи с первым примером, после выполнения преобразований в расширенной матрице системы могли появиться строки вида
соответствующие уравнению вида
Если среди них есть хотя бы одно уравнение с отличным от нуля свободным членом (т.е. ), то данная система уравнений является несовместной, то есть не имеет решений и на этом её решение закончено.
Пример 7. Решить методом Гаусса систему линейных уравнений:
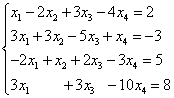
Решение. Составляем расширенную матрицу системы. С помощью первого уравнения исключаем из последующих уравнений переменную . Для этого ко второй строке прибавляем первую, умноженную на , к третьей строке - первую, умноженную на , к четвёртой - первую, умноженную на .
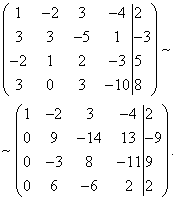
Теперь нужно с помощью второго уравнения исключить переменную из последующих уравнений. Чтобы получить целые отношения коэффициентов, поменяем местами вторую и третью строки расширенной матрицы системы.
Для исключения из третьего и четвёртого уравнения к третьей строке прибавим вторую, умноженную на , а к четвёртой - вторую, умноженную на .
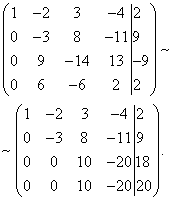
Теперь с помощью третьего уравнения исключим переменную из четвёртого уравнения. Для этого к четвёртой строке прибавим третью, умноженную на .
Заданная система эквивалентна, таким образом, следующей:
Полученная система несовместна, так как её последнее уравнение не может быть удовлетворено никакими значениями неизвестных. Следовательно, данная система не имеет решений.
Метод Гаусса – метод последовательного исключения неизвестных – заключается в том, что с помощью элементарных преобразований исходная система приводится к равносильной ей системе ступенчатого или треугольного вида, из которой последовательно, начиная с последних (по номеру), неизвестных находятся все остальные неизвестные. Дана система (1)
Начинаем осуществлять прямой ход . Считаем, что коэффициент а 11 ≠ 0; если же это не так, меняем местами уравнения.
Первый
шаг состоит в том, чтобы исключить
неизвестное х
1
из всех уравнений, кроме первого. Для
этого ко второму уравнению прибавим
первое уравнение, умноженное на число
,
к третьему уравнению прибавим первое
уравнение, умноженное на число
,
и так далее до последнего уравнения.
После первого шага получим систему:
Полученная система равносильна исходной системе.
Вторым
шагом исключают неизвестное из всех
уравнений, кроме первого и второго. Для
этого повторяем все действия первого
шага для второго и последующих уравнений,
а именно: считаем, что коэффициент
≠ 0
и так далее. Если в результате преобразований
получается нулевое уравнение, то его
удаляют, если же получается несовместное
уравнение, то решение системы закончено
– она несовместна. Процесс исключения
неизвестных продолжаем до тех пор, пока
это возможно. Обозначим количество
уравнений, оставшихся после прямого
хода, через r
.
Это число равно рангу основной матрицы
системы и может быть меньше или равно
n
.
Рассмотрим оба случая.
1) Если r = n
где с 11 ≠ 0, с 22 ≠ 0, …, с nn ≠ 0.
Обратным
ходом
,
начиная с последнего уравнения,
последовательно найдем значения x
n
,
(где x
n
= 
),
x
n
– 1 ,
..., x
1 .
В этом случае система линейных уравнений
имеет единственное решение, то есть
является определенной.
2) Если r < n , то система после прямого хода принимает вид:
где с 11 ≠ 0, с 22 ≠ 0, …, с rr ≠ 0. Неизвестные x 1 , x 2 , …, x r , с которых начинаются уравнения, называются главными неизвестными , а остальные x r + 1 , x r + 2 , …, x n – свободными . В этом случае обратным ходом, начиная с последнего уравнения, выражают главные неизвестные через свободные неизвестные. Получают следующие равенства:
x 1 = k 1, r + 1 x r + 1 + … + k 1, n x n + t 1 ,
x 2 = k 2, r + 1 x r + 1 + … + k 2, n x n + t 2 ,
……………………………………..
x r = k r , r + 1 x r + 1 + … + k r , n x n + t r .
Определение 6.10. Общим решением системы называется выражение главных неизвестных через свободные.
Если свободным неизвестным придать какие-нибудь числовые значения, то из общего решения получим значения главных неизвестных. Таким образом, получают частное решение системы. Из способа его получения следует, что система имеет более одного решения, то есть является неопределенной.
Пример 6.3. Решить методом Гаусса систему линейных уравнений:
Решение
.
Преобразования
с системой линейных удобнее производить
не с самими уравнениями, а с матрицей
их коэффициентов. Расширенная матрица
этой системы имеет вид: (А
|B
) = 
.
Осуществляем
прямой ход. Первым шагом исключаем
неизвестное х
1
из всех уравнений, кроме первого. Так
как а
11 = 1 ≠ 0,
то переставлять уравнения местами не
нужно. Прибавим ко второму уравнению
системы первое уравнение, умноженное
на (–1), к третьему уравнению – первое,
умноженное на (–3). Получим после
преобразований следующую матрицу:
,
в которой элемент а
22 = 1.
Перестановка местами уравнений (первое
уравнение трогать не следует) не поможет,
поэтому переходим к следующему
неизвестному х
3
и исключаем его из всех уравнений, кроме
первого и второго. Для этого к третьему
уравнению прибавим второе, умноженное
на (–2) и вычеркнем получившееся нулевое
уравнение. После прямого хода получаем
следующую систему:
.
Прямой ход завершен. В этом случае n
= 4,
r
= 2,
r
< n
,
и, следовательно, система неопределенная.
Главные неизвестные – это те неизвестные,
с которых начинаются уравнения, в нашем
случае это х
1
и х
3 .
Неизвестные х
2
и х
4
– свободные.
Обратным
ходом надо выразить главные неизвестные
через свободные. Для этого в столбцах,
содержащих ведущие элементы строк,
следует получить нули. Здесь это элемент
а
13 .
Прибавим к первому уравнению, умноженному
на 2, второе и выпишем получившуюся
матрицу коэффициентов:
,
а затем и сами уравнения:
Из
этих уравнений получаем общее решение:
Найдем
какое-нибудь частное решение; пусть
х
2 = 3,
х
4 = 1,
тогда из общего решения получим значения
х
1 = 
,
и х
1 = –2.
Таким образом, частное решение – вектор
а
= (
,
3, –2, 1).
Ответ
:
общее решение {(
,
х
2 ,
,
х
4)},
где х
2 ,
х
4 R;
частное
решение, если х
2 = 3,
х
4 = 1,
то (
,
3, –2, 1).
Рассмотрим один из самых распространенных методов решения систем линейных алгебраических уравнений - метод Гаусса. Этот метод (который называют также методом последовательного исключения неизвестных) известен в различных вариантах уже более 2000 лет.
Вычисления с помощью метода Гаусса состоят из двух основных этапов, называемых прямым ходом и обратным ходом (обратной подстановкой). Прямой ход метода Гаусса заключается в последовательном исключении неизвестных из системы (5.1) для преобразования ее к эквивалентной системе с верхней треугольной матрицей. Вычисления значений неизвестных производят на этапе обратного хода.
1. Схема единственного деления.
Рассмотрим сначала простейший вариант метода Гаусса, называемый схемой единственного деления.
Прямой ход состоит из шагов исключения.
1-й шаг. Целью этого шага является исключение неизвестного из уравнений с номерами Предположим, что коэффициент Будем называть его главным (или ведущим) элементом 1-го шага.
Найдем величины
называемые множителями 1-ю шага. Вычтем последовательно из второго, третьего, уравнений системы (5.1) первое уравнение, умноженное соответственно на Это позволит обратить в
нуль коэффициенты при во всех уравнениях, кроме первого. В результате получим эквивалентную систему
в которой вычисляются по формулам
2-й шаг. Целью этого шага является исключение неизвестного из уравнений с номерами Пусть где - коэффициент, называемый главным (или ведущим) элементом шага. Вычислим множители 2-го шага
и вычтем последовательно из третьего, четвертого, уравнений системы (5.30) второе уравнение, умноженное соответственно на . В результате получим систему
Здесь коэффициенты вычисляются по формулам
Аналогично проводятся остальные шаги. Опишем очередной шаг.
k-й шаг. В предположении, что главный (ведущий) элемент шага отличен от нуля, вычислим множители шага
и вычтем последовательно из уравнений полученной на предыдущем шаге системы уравнение, умноженное соответственно на
После шага исключения получим систему уравнений
матрица которой является верхней треугольной. На этом вычисления прямого хода заканчиваются.
Обратный ход. Из последнего уравнения системы (5.33) находим Подставляя найденное значение в предпоследнее уравнение, получим Осуществляя обратную подстановку, далее последовательно находим Вычисления неизвестных здесь проводятся по формулам
Трудоемкость метода. Оценим число арифметических операций, необходимых для реализации схемы единственного деления.
Вычисления 1-го шага исключения по формулам (5.29), (5.31) требуют выполнения деления, умножений и вычитаний, т. е. общее число арифметических операций составляет Аналогично, на шаге требуется операций, а на шаге - операций.
Подсчитаем теперь приближенно общее число арифметических операций прямого хода, считая размерность системы достаточно большой:
Как нетрудно видеть, для реализации обратного хода по формулам (5.34) нужно всего операций, что при больших пренебрежимо мало по сравнению с числом операций прямого хода.
Таким образом, для реализации метода Гаусса требуется примерно арифметических операций, причем подавляющее число этих действий совершается на этапе прямого хода.
Пример 5.7. Методом Гаусса решим систему
Прямой ход. 1-й шаг. Вычислим множители Вычитая из второго, третьего и четвертого уравнений системы (5.35) первое уравнение, умноженное на соответственно получим
2-й шаг. Вычислим множители Вычитая из третьего и четвертого уравнений системы (5.36) второе уравнение, умноженное на соответственно, приходим к системе
3-й шаг. Вычисляя множитель и вычитая из четвертого уравнения системы (5.37) третье уравнение, умноженное на приводим систему к треугольному виду:
Обратный ход. Из последнего уравнения системы находим Подставляя значение в третье уравнение, находим
Результаты вычислений можно свести в следующую таблицу.
Таблица 5.2 (см. скан)
Необходимость выбора главных элементов. Заметим, что вычисление множителей, а также обратная подстановка требуют деления на главные элементы Поэтому если один из главных элементов сказывается равным нулю, то схема единственного деления не может быть реализована. Здравый смысл подсказывает, что и в ситуации, когда все главные элементы отличны от нуля, но среди них есть близкие к нулю, возможен неконтролируемый рост погрешности.
Пример 5.8. Используя метод Гаусса, решим систему уравнений
на -разрядной десятичной ЭВМ.
Прямой ход. 1-й шаг. Вычисляем множители и преобразуем систему к виду
Все вычисления на этом шаге выполняются без округлений.
2-й шаг. После вычисления множителя последнее уравнение системы должно быть преобразовано к виду где Однако на используемой ЭВМ будет получено уравнение
Действительно, коэффициент определяется точно, так как при его вычислении не возникает чисел, мантиссы которых имеют более 6 разрядов. В то же время при вычислении умножение коэффициента 3.0001 на дает 7-разрядное число 105003.5, после округления которого до 6 разрядов получится 105004. Вычисление 62) завершается выполнением операции вычитания: . После округления последнего числа до 6 разрядов мантиссы приходим к уравнению (5.41).
Обратный ход. Из уравнения (5.41) находим и 1.00001. Сравнение с истинным значением показывает, что эта величина получена с очень высокой для используемой ЭВМ точностью. Дальнейшие вычисления дают
После округления имеем .
Как нетрудно видеть, найденные значения неизвестных имеют мало общего с истинными значениями решения
В чем же причина появления такой значительной погрешности? Говорить о накоплении ошибок округления не приходится, так как всего было выполнено 28 арифметических операций и лишь в 4 случаях потребовалось округление. Предположение о плохой обусловленности системы не подтверждается; вычисление дает значение и 100.
В действительности причина состоит в использовании на шаге малого ведущего элемента Следствием этого стало появление большого
множителя и существенное возрастание коэффициента в последнем уравнении системы.
Таким образом, изложенный выше вариант метода Гаусса (схема единственного деления) оказался некорректным и, следовательно, непригодным для вычислений на ЭВМ. Этот метод может привести к аварийному останову (если при некотором и вычисления по нему могут оказаться неустойчивыми.
2. Метод Гаусса с выбором главного элемента по столбцу (схема частичного выбора).
Описание метода. На шаге прямого хода коэффициенты уравнений системы с номерами преобразуются по формулам
Интуитивно ясно, что во избежание сильного роста коэффициентов системы и связанных с этим ошибок нельзя допускать появления больших множителей
В методе Гаусса с выбором главного элемента по столбцу гарантируется, что для всех к Отличие этого варианта метода Гаусса от схемы единственного деления заключается в том, что на шаге исключения в качестве главного элемента выбирают максимальный по модулю коэффициент а. при неизвестной в уравнениях с номерами Затем соответствующее выбранному коэффициенту уравнение с номером меняют местами с уравнением системы для того, чтобы главный элемент занял место коэффициента
После этой перестановки исключение неизвестного производят, как в схеме единственного деления.
Пример 5.9. Решим систему уравнений (5.39) методом Гаусса с выбором главного элемента по столбцу на -разрядной десятичной ЭВМ.
Прямой ход. 1-й шаг. Максимальный в первом столбце элемент матрицы находится в первой строке, поэтому перестановка уравнений не нужна. Здесь 1-й шаг проводится точно так же, как и в примере 5.8.
2-й шаг. Среди элементов матрицы системы (5.40) максимальный принадлежит третьему уравнению. Меняя местами второе и третье уравнения, получим систему
После вычисления последнее уравнение системы преобразуется к виду
Обратный ход. Из последнего уравнения находим Далее, имеем В данном случае ответ получился точным.
Заметим, что дополнительная работа по выбору главных элементов в схеме частичного выбора требует порядка действий, что практически не влияет на общую трудоемкость метода.
Вычислительная устойчивость схемы частичного выбора. Детальное исследование метода Гаусса показывает, что действительной причиной неустойчивости схемы единственного деления является возможность неограниченного роста элементов промежуточных матриц в процессе прямого хода. Так как на шаге схемы частичного выбора 1, то для вычисленных по формулам (5.42) элементов справедлива оценка Следовательно, максимальное по модулю значение элементов матрицы возрастает на одном шаге не более чем в 2 раза и в самом неблагоприятном случае шаг прямого хода даст коэффициент роста
Гарантия ограниченности роста элементов матрицы делает схему частичного выбора вычислительно устойчивой. Более того, для нее оказывается справедливой следующая оценка погрешности:
Здесь вычисленное на ЭВМ решение системы; его относительная погрешность; число обусловленности матрицы ем - машинное эпсилон; наконец, причем некоторая медленно растущая функция, зависящая от порядка системы (типа степенной функции с небольшим показателем), коэффициент роста.
Наличие в оценке (5.43) множителя указывает на то, что при большом схема частичного выбора может оказаться плохо обусловленной и возможна существенная потеря точности. Однако практика матричных вычислений показывает, что существенный рост элементов матрицы происходит крайне редко. В подавляющем большинстве случаев действительное значение коэффициента роста не превышает 8-10. Если система хорошо обусловлена, то погрешность вычисленного решения оказывается, как правило, малой.
Иногда для проверки качества приближенного решения х
вычисляют невязку и о степени близости приближенного решения к точному пытаются судить по тому, насколько мала невязка. Этот метод ненадежен по отношению к схеме частичного выбора, так как известно, что она гарантированно дает малые невдэки. Более точно это утверждение можно сформулировать так: справедлива оценка
где то же, что и в оценке (5.43). Заметим, что в неравенство (5.44) не входит число обусловленности.
3. Метод Гаусса с выборок главного элемента по всей матрице (схема полного выбора).
В этой схеме допускается нарушение естественного порядка исключения неизвестных.
На 1-м шаге метода среди элементов определяют максимальный по модулю элемент Первое уравнение системы и уравнение с номером меняют местами. Далее стандартным образом производят исключение неизвестного х, из всех уравнений, кроме первого. (что значительно меньше соответствующего значения для схемы частичного выбора). Подчеркнем, что до сих пор еще не найдено матрицы, для которой полный выбор дал бы значение Таким образом, для хорошо обусловленных систем этот вариант метода Гаусса является хорошо обусловленным.
Однако гарантия хорошей обусловленности достигается здесь ценой значительных затрат на выбор главных элементов. Для этого дополнительно к арифметических действий требуется произвести примерно операций сравнения, что может ощутимо замедлить процесс решения задачи на ЭВМ. Поэтому в большинстве случаев на практике предпочтение отдается все же схеме частичного выбора. Как уже отмечено, ситуации, когда при использовании этого варианта метода Гаусса происходит существенный рост элементов, встречаются чрезвычайно редко. Более того, эти ситуации могут быть легко выявлены с помощью заложенных в современных программах эффективных методов слежения за ростом элементов матриц.
4. Случаи, когда выбор главных элементов не нужен.
Известно, что для некоторых классов матриц при использовании схемы единственного деления главные элементы гарантированно располагаются на главной диагонали и потому применять частичный выбор нет необходимости. Так, например, обстоит дело для систем с положительно определенными матрицами, а также с матрицами, обладающими следующим свойством диагонального преобладания:
Матрицы, удовлетворяющие условию (5.45), таковы, что в каждой из строк модуль элемента расположенного на главной диагонали, больше суммы модулей всех остальных элементов строки.
5. Масштабирование.
Перед началом решения целесообразно масштабировать систему так, чтобы ее коэффициенты были величинами порядка единицы.
Существуют два естественных способа масштабирования системы Первый заключается в умножении каждого из уравнений на некоторый масштабирующий множитель Второй состоит в умножении на масштабирующий множитель каждого столбца матрицы, что соответствует замене переменных (фактически - это замена единиц измерения). В реальных ситуациях чаще всего масштабирование может быть выполнено без существенных трудностей. Однако подчеркнем, что в общем случае удовлетворительного способа масштабирования пока не найдено.
На практике масштабирование обычно производят с помощью деления каждого уравнения на его наибольший по модулю коэффициент. Это вполне удовлетворительный способ для большинства реально встречающихся задач.
Пусть дана система , ∆≠0. (1)Метод Гаусса – это метод последовательного исключения неизвестных.
Суть метода Гаусса состоит в преобразовании (1) к системе с треугольной матрицей , из которой затем последовательно (обратным ходом) получаются значения всех неизвестных. Рассмотрим одну из вычислительных схем. Эта схема называется схемой единственного деления. Итак, рассмотрим эту схему. Пусть a 11 ≠0 (ведущий элемент) разделим на a 11 первое уравнение. Получим
(2)
Пользуясь уравнением (2), легко исключить неизвестные x 1 из остальных уравнений системы (для этого достаточно из каждого уравнения вычесть уравнение (2) предварительно умноженное на соответствующий коэффициент при x 1), то есть на первом шаге получим
.
Иными словами, на 1 шаге каждый элемент последующих строк, начиная со второй, равен разности между исходным элементом и произведением его «проекции» на первый столбец и первую (преобразованную) строку.
Вслед за этим оставив первое уравнение в покое, над остальными уравнениями системы, полученной на первом шаге, совершим аналогичное преобразование: выберем из их числа уравнение с ведущим элементом и исключим с его помощью из остальных уравнений x 2 (шаг 2).
После n шагов вместо (1) получим равносильную систему
(3)
Таким образом, на первом этапе мы получим треугольную систему (3). Этот этап называется прямым ходом.
На втором этапе (обратный ход) мы находим последовательно из (3) значения x n , x n -1 , …, x 1 .
Обозначим полученное решение за x 0 . Тогда разность ε=b-A·x 0 называется невязкой
.
Если ε=0, то найденное решение x 0 является верным.
Вычисления по методу Гаусса выполняются в два этапа:
- Первый этап называется прямым ходом метода. На первом этапе исходную систему преобразуют к треугольному виду.
- Второй этап называется обратным ходом. На втором этапе решают треугольную систему, эквивалентную исходной.
На каждом шаге предполагалось, что ведущий элемент отличен от нуля. Если это не так, то в качестве ведущего можно использовать любой другой элемент, как бы переставив уравнения системы.
Назначение метода Гаусса
Метод Гаусса предназначен для решения систем линейных уравнений. Относится к прямым методам решения.Виды метода Гаусса
- Классический метод Гаусса;
- Модификации метода Гаусса. Одной из модификаций метода Гаусса является схема с выбором главного элемента. Особенностью метода Гаусса с выбором главного элемента является такая перестановка уравнений, чтобы на k -ом шаге ведущим элементом оказывался наибольший по модулю элемент k -го столбца.
- Метод Жордано-Гаусса;
Проиллюстрируем отличие метода Жордано-Гаусса от метода Гаусса на примерах.
Пример решения методом Гаусса
Решим систему:
Для удобства вычислений поменяем строки местами:
Умножим 2-ую строку на (2). Добавим 3-ую строку к 2-ой
Умножим 2-ую строку на (-1). Добавим 2-ую строку к 1-ой
Из 1-ой строки выражаем x 3:
Из 2-ой строки выражаем x 2:
Из 3-ой строки выражаем x 1: 
Пример решения методом Жордано-Гаусса
Эту же СЛАУ решим методом Жордано-Гаусса.
Последовательно будем выбирать разрешающий элемент РЭ, который лежит на главной диагонали матрицы.
Разрешающий элемент равен (1).
НЭ = СЭ - (А*В)/РЭ
РЭ - разрешающий элемент (1), А и В - элементы матрицы, образующие прямоугольник с элементами СТЭ и РЭ.
Представим расчет каждого элемента в виде таблицы:
| x 1 | x 2 | x 3 | B |
| 1 / 1 = 1 | 2 / 1 = 2 | -2 / 1 = -2 | 1 / 1 = 1 |
 |  |  |  |
Разрешающий элемент равен (3).
На месте разрешающего элемента получаем 1, а в самом столбце записываем нули.
Все остальные элементы матрицы, включая элементы столбца B, определяются по правилу прямоугольника.
Для этого выбираем четыре числа, которые расположены в вершинах прямоугольника и всегда включают разрешающий элемент РЭ.
| x 1 | x 2 | x 3 | B |
 |  |
||
| 0 / 3 = 0 | 3 / 3 = 1 | 1 / 3 = 0.33 | 4 / 3 = 1.33 |
 |
Разрешающий элемент равен (-4).
На месте разрешающего элемента получаем 1, а в самом столбце записываем нули.
Все остальные элементы матрицы, включая элементы столбца B, определяются по правилу прямоугольника.
Для этого выбираем четыре числа, которые расположены в вершинах прямоугольника и всегда включают разрешающий элемент РЭ.
Представим расчет каждого элемента в виде таблицы:
| x 1 | x 2 | x 3 | B |
 |  |  |  |
 |  |
||
| 0 / -4 = 0 | 0 / -4 = 0 | -4 / -4 = 1 | -4 / -4 = 1 |
Ответ : x 1 = 1, x 2 = 1, x 3 = 1